Prisma óptico: entenda na Óptica geométrica
Prisma óptico se formam de uma substância transparente como vidro ou orgânicos for feita com planos que se cruzam e formam um ângulo, ou seja, laminados e mais grossos, teremos um prisma.
Um prisma com duas faces planas de refração, um ângulo incluído e um ângulo de vértice entre as duas faces. As superfícies dos prismas também podem ser curvas, especialmente quando feitas para óculos.

Os prismas não apenas desviam um feixe de luz para suas bases, se a luz é composta, ela divide a luz em um espectro de cores diferentes. Essa quebra de luz é chamada de “dispersão”.
Uso dos prismas:
O uso de prismas nada tem a ver com a clareza do próprio objeto visualizado. Os prismas corrigem a foria, o estrabismo ou os distúrbios da visão binocular. No caso acima, o prisma facilita a superposição das imagens vistas pelos dois olhos e não proporciona nitidez.
Desvio do prisma:
A luz que passa pelo prisma tem uma direção diferente da luz que entra nele. Isso ocorre porque as duas superfícies não são paralelas. Eles são em forma de cunha, e o poder de refração de um prisma depende do ângulo formado pelas duas superfícies.
Ângulo de refração:
O ângulo de refração de um prisma é pequeno, geralmente não mais que 15° ou 20°. Os prismas são geralmente redondos ou quadrados, em ângulo reto ou equilátero, e são usados em óculos para corrigir a foria, medições de dioptria para avaliar estrabismo e trabalhos corretivos.
Dioptria Prismática:
A unidade de medida para prismas é “dioptria de prisma”, criada por Charles F. Prentice em 1888. É uma medida do desvio da luz produzida por um determinado prisma sob um conjunto de condições, dioptria do prisma é agora a notação universal. para prismas.
A dioptria do prisma, cujo símbolo é um triângulo com a base voltada para baixo, (Δ) representa a potência do prisma necessária para produzir um centímetro de desvio de luz, estando os prismas separados por uma distância de um metro. Da mesma forma, um prisma de Δ 3,00 produz um desvio de 3 cm em uma escala tangente a um metro.
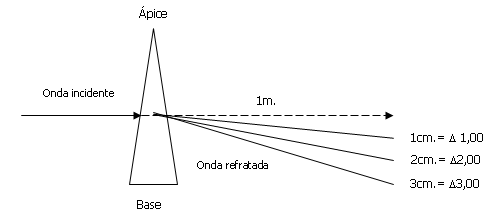
Deslocamento aparente dos objetos através do prisma
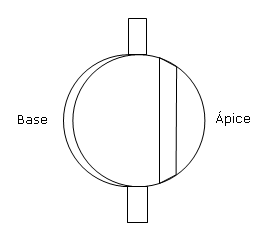
O deslocamento significativo do objeto ocorre no ápice à medida que a luz é desviada para o fundo. Se você olhar para um objeto junto com uma coluna, verá que ele se move para a borda mais fina (vértice).
Medidas antigas dos prisma óptico
No passado, os prismas eram medidos em “graus” ou “centros”. O termo “dioptria de prisma” é usado com frequência crescente e agora é usado internacionalmente. O símbolo para “centrado” é um delta com seu vértice para baixo N.
A medição do grau torna-se impraticável devido à imprecisão e impraticabilidade. O sistema centrado é mais preciso que o sistema de Prentice. Dennett demonstrou que a centralização é mais precisa, principalmente em relação à formação do arco, e os prismas também são medidos em dioptrias prismáticas.
Como o sistema baseado em tangente se mostrou mais prático, já que o desvio óptico é um múltiplo do desvio produzido por um prisma de 1,00 dioptrias, a medição dos valores dos prismas pode ser realizada com mais facilidade, principalmente em um medidor de lentes.
Um prisma de 10,00 dioptrias é duas vezes mais capaz de dobrar a luz do que um prisma de 5,00 dioptrias.
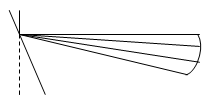
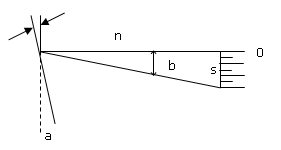
Para medições de prisma, use a escala Prentice ou a escala tangente. Isso inclui gráficos (P) a uma distância (n) da barra de escala (S). A régua é dividida em unidades de dioptria prismáticas com intervalos de (n) cm.
A linha zero (0) na escala é uma linha acima das outras linhas. Coloque o prisma a ser medido contra o desenho (P) com sua face paralela à régua e sua base (n) paralela à régua. A linha 0 é observada através de um prisma, sua posição é lida com referência a uma escala fora do prisma e o resultado é expresso diretamente em dioptrias do prisma ou em frações obtidas.
A maioria das réguas de medição são usadas para distâncias de 3, 5 ou 6 metros.
No passado, os prismas eram medidos em “centros” ou graus, e ainda hoje os termos “dioptrias do prisma” e “graus” são usados alternadamente, o que é impreciso porque os prismas são anotados em graus para o período do ângulo do vértice.
Em 1801, Dennett propôs uma medida de potência diferenciada (centralizada) com o símbolo Ñ, o delta de baixo para cima.
Principalmente essas medidas são as mesmas sugeridas pelo Sr. Prentice, exceto que as medições são feitas em arcos em vez de tangentes. Em teoria, o centroide é mais preciso devido às bissetrizes implícitas dos equiângulos ao medir prismas. Isso não é verdade para a escala Prentice.
No entanto, para prismas oftálmicos, as duas unidades são semelhantes, e a potência do prisma agora é usada como padrão, principalmente porque o desvio óptico de qualquer potência do prisma é um múltiplo do desvio produzido por Δ 1,00. Δ 10,00 é duas vezes mais capaz de dobrar a luz do que Δ 5,00 ao usar o sistema Prentice.
Ângulo apical
Para calcular o ângulo do vértice (a) de um prisma, uma certa potência do prisma precisa ser gerada e o desvio ou ângulo (b) precisa ser calculado primeiro. A partir do gráfico da página anterior, isso é verdade porque:
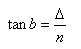
Nesta equação, (Δ) e (n) são expressos na mesma unidade, como centímetros, metros ou polegadas.
Conhecendo o índice de refração (nd) do material, a seguinte relação dará a tangente do ângulo (a), referente à tabela trigonométrica, e dará o valor de (a) em graus. Se o prisma for de vidro com índice de refração (nd) = 1,523, este será o ângulo do vértice necessário para produzir a potência prismática predeterminada.
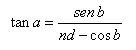
Cálculo do ângulo apical
O ângulo do ápice é refratado pelas duas superfícies e forma um ângulo chamado “ângulo do ápice”.
Para calcular o ângulo do vértice do prisma (a) necessário para produzir uma certa potência do prisma, primeiro você precisa calcular o desvio ou ângulo (B). do seguinte modo:
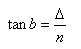
Os valores de dioptria do prisma e os ângulos do ápice de prismas oftálmicos comuns são mostrados na tabela abaixo:
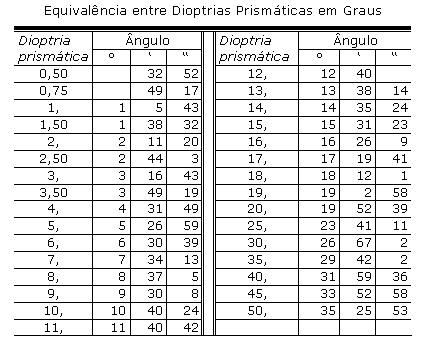
Diferença de Espessuras entre Bordos (mm) para prismas de vidro com índice 1,523 (vidro Comum-Crown)
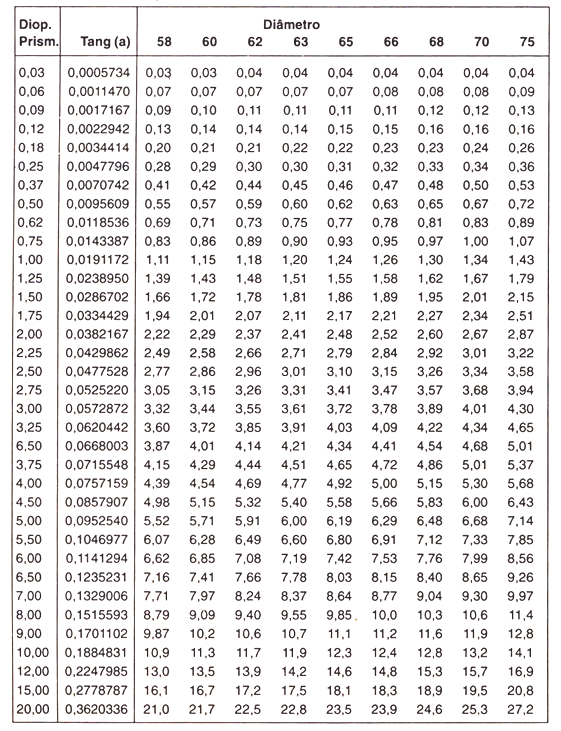
Diferença de espessuras para outros índices de refração
A tabela acima foi elaborada para blocos de diferentes diâmetros, utilizando um bloco com índice de refração de 1,523 (Coroa). Se você precisar usar minerais ou lentes orgânicas com um índice diferente de 1,523, uma aproximação segura pode ser obtida multiplicando os números fornecidos na tabela por:
K=1,048 para (nd) = 1,499 – Resina CR39
K= 0,849 para (nd) = 1,616 – Bário ou Flint
K= 0,785 para (nd) = 1,666 – Resina de médio índice
K= 0,758 para (nd) = 1,690 – Resina de alto índice
K= 0,746 para (nd) = 1,701 – Vidro alto índice
Para calcular uma outra constante (K) para índices não relacionados acima, usem:
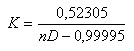
Na tabela acima mostramos uma indicação da diferença de espessura entre as arestas, o índice nD 1,523, que é necessário para fabricar prismas de D 0,03 dioptrias de prisma a D 20,00
O diâmetro do bloco é de 58 mm. até 75mm. A tabela já mostra (a) a tangente em relação ao índice nD 1,523.
A tabela acima fornece aos oculistas profissionais uma nova dimensão e compreensão dos prismas. Obviamente, é mais útil para especialistas em fabricação de lentes que trabalham em um laboratório.
exemplo:
Se você deseja calcular a diferença entre as bordas da lente prismática e outro índice não incluído na tabela acima, use o seguinte procedimento:
Rx: D 4,00 com diâmetro de 50 mm.
Multiplique a tangente da tabela (a) acima por D 4,00 (0,0757150) por 50 (diâmetro e teremos 3,79mm. Isso é cerca de 3,8mm. Esta será a diferença entre as arestas feitas no bloco de 50mm, 4,00 Prisma de prismático dioptria.
Outro exemplo da lente de alto índice nD 1.701:
Rx: D 3,00, diâmetro 65mm.
Observe que na tabela acima, para um índice nD de 1,523, a diferença de espessura entre as bordas é de 3,72mm. Multiplicando 3,72 pela constante dada em relação ao expoente 1,701 (0,746) resulta em 2,77.
Portanto, para fazer um prisma de 3,00 dioptrias, em um vidro mineral com índice nD 1,701, é necessária uma diferença de 2,8 mm entre as bordas.
Dois prisma óptico cruzados perpendicularmente resultam num único prisma, com base definida
Se você receber uma receita com dois prismas que se cruzam verticalmente (90º entre as duas bases), os dois prismas podem resultar em um prisma com uma base.
Suponha que RX (abreviatura de receita) signifique:
Base superior Oh Prism 4.00 combinada com base externa prisma 5.00. Esta receita resultará em:
Como calcular? Usaremos soluções vetoriais e gráficas.
- Um prisma prescrito pode ser representado por dois vetores cuja magnitude corresponde ao valor do prisma prescrito.
- Usando esses valores e a diferença angular entre eles, trace o gráfico em uma escala (em polegadas ou centímetros) conforme o diagrama a seguir:
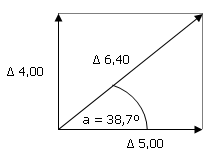
Onde:
- Δ 4,00 e Δ 5,00 são os valores especificados do prisma, do ápice até a base do prisma, reutilizamos valores em centímetros ou polegadas.
- A = é a diferença entre os ângulos dos prismas especificados.
Exemplo:
Neste caso temos um prisma de 4,00 diops. Com base superior e outro prisma de 5,00 dioptrias. com base externa para corrigir a ortografia. O prisma 4.00 é representado por um vetor com 4 unidades de comprimento (por exemplo, 4 cm), e o prisma 5.00 também é representado por outro vetor com 5 unidades de comprimento (por exemplo, 5 cm).
O ângulo entre esses dois vetores é desenhado com um transferidor de 90º.
Pode-se ver que o sistema de análise vetorial pode ser usado para resolver prismas que se cruzam verticalmente.
O comprimento do vetor pode ser medido em qualquer unidade, como centímetros ou polegadas.
Complete o retângulo como mostrado acima e desenhe o vetor diagonal (resultado) que, quando medido nas mesmas unidades, dará Δ 6,40 nas mesmas unidades de comprimento.
Portanto, o prisma resultante será Δ 6,40 dioptrias. Prisma.
Meça o ângulo (a) com um transferidor e o problema está resolvido.
A receita convertida será:
Δ 6,40 dioptrias. Com base superior externa 38,7°
Conclusão: Dois prismas cruzados verticalmente criarão uma nova base para outro prisma e um novo eixo.
Se você quiser, se os prismas se cruzam em ângulos retos, o ângulo (a) é 90° e o cosseno de 90° é zero, podemos usar:
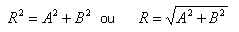
Combinação de dois prismas ópticos cruzados perpendicularmente
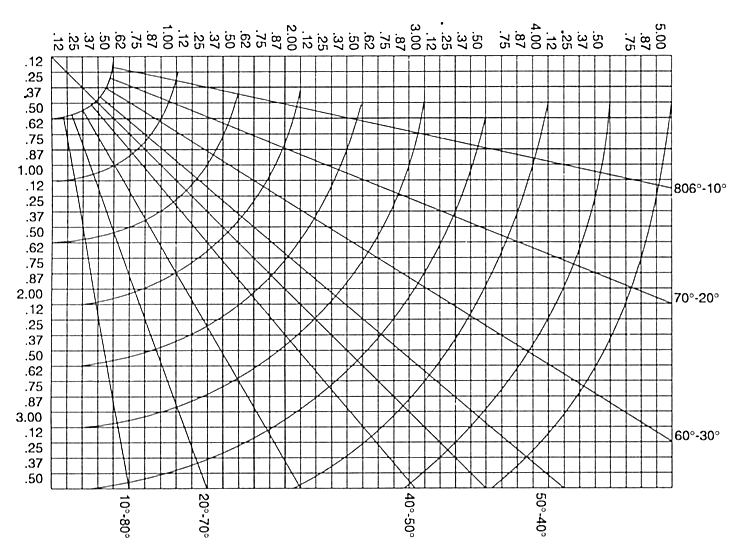
Se você deseja sintetizar rapidamente a combinação vertical (90°) de dois números primos sem cálculos, consulte a tabela abaixo e siga os passos abaixo:
A partir da interseção de dois prismas de interseção conhecidos, siga a curva até a borda do gráfico para determinar o prisma resultante. Conecte essa interseção ao “O” do gráfico e leia o valor do ângulo do prisma resultante com um transferidor, que será o ângulo entre essa linha formada e a aresta correspondente ao maior prisma.
Prisma por descentração do centro óptico
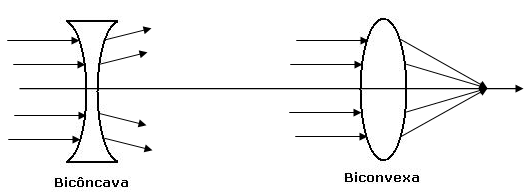
Uma lente pode ser pensada como uma combinação de dois prismas que estão conectados na base (positivo) e no ápice (negativo).
Os valores prismáticos aumentam gradualmente, em direção à periferia. Não há prisma no centro óptico da lente porque as superfícies são paralelas.
Por exemplo:
Para calcular a potência prismática, basta usar a seguinte fórmula:
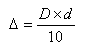
Sendo:
- 🔺 = dioptria prismática
- D= Dioptria da lente
- d = Descentração do centro óptico em mm.
Regras básicas para excentricidade de lentes de 1,00 dioptrias. esf., um deslocamento de 1cm (10mm) produzirá uma potência prismática de D 1,00.
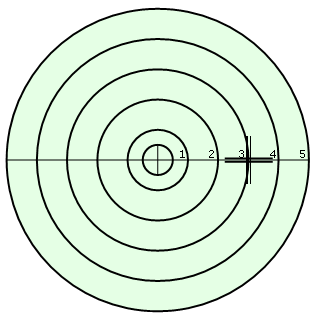
Para calcular quantos milímetros de descentralização a lente acabada precisa ter para obter determinados valores de prisma, a seguinte fórmula é usada:
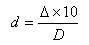
Isso significa que, com uma lente de prateleira, poderemos obter um prisma simplesmente descentralizando o centro óptico na lente.
Use um lensômetro e fala descentralização da luneta para o círculo correspondente ao prime desejado e marque o novo centro onde o montador irá montar a lente de acordo com o DP do cliente.
A tabela indica o mm necessário para obter o prisma mostrado na coluna superior
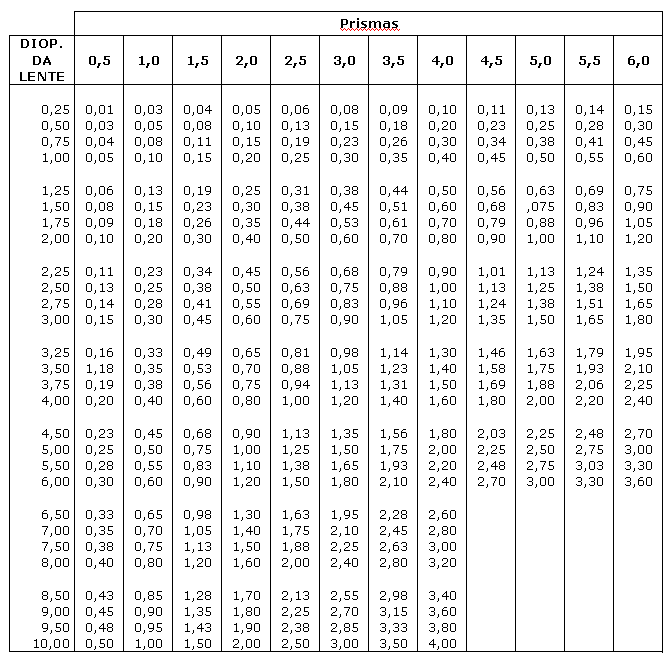
RESOLUÇÃO DE PRISMAS COMBINADOS DE RECEITUÁRIO
Às vezes, na óptica oftálmica, é necessário um certo número de prismas de correção para abordar o equilíbrio vertical (foria) e o equilíbrio horizontal separadamente e corrigi-los separadamente.
Dois ou mais prismas aplicados, que se cruzam em qualquer ângulo, são equivalentes a um único prisma ou prisma, cujo valor depende da potência de cada prisma e do ângulo entre eles. A solução para encontrar o prisma final é simples e envolve prismas que se cruzam perpendicularmente ou obliquamente.
Provavelmente a solução mais simples e compreensível para este tipo de problema é obtida por meio da análise “vetorial”, um vetor é uma seta cuja magnitude e direção correspondem à linha de base do vértice do prisma. A direção da seta sempre aponta para a base do prisma.
Use um transferidor, régua e papel para resolver qualquer problema de prisma cruzado, juntamente com os seguintes exemplos:
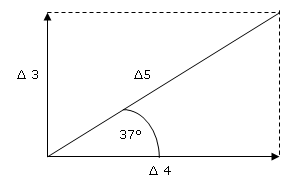
Exemplo: Neste caso, dois prismas precisam ser combinados, um Δ 3,00 com base superior e outro Δ 4,00 com base externa para corrigir orto. Use um vetor de 3 unidades de comprimento para ∆ 3,00 base para cima e outro vetor de 4 unidades para ∆ 4,00 base para cima. O ângulo entre esses dois vetores é de 90° desenhado no transferidor. O comprimento pode ser medido em qualquer unidade, como centímetros ou polegadas, para fornecer a mesma unidade para medir a hipotenusa e todo o problema. Complete o esboço do paralelogramo e desenhe um vetor diagonal (R) que mede 5 unidades de comprimento.
Portanto, o prisma resultante será Δ 5,00. Meça o ângulo com o mesmo transferidor e o problema está resolvido. O RX resultante será: Δ 5,00 com um ângulo de base maior que 37°.
Prismas Cruzados Obliquamente
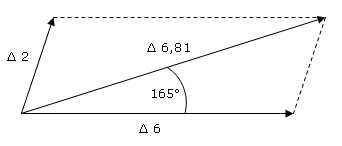
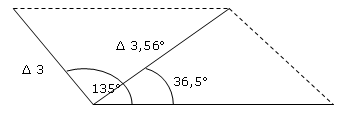
Outros problemas de prisma mostrando construção de prisma cruzado oblíquo são mostrados na imagem acima, e os tornamos públicos, e pode-se ver que a solução é simples quando o método de análise “vetorial” é seguido.
Para aqueles prismas que favorecem matematicamente a expressão de prisma produzida por quaisquer dois prismas de interseção, veja o seguinte:
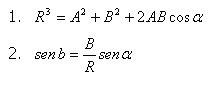
Nestas equações, os símbolos têm os seguintes significados:
A = Poder dióptrico de um dos prismas
B = Poder dióptrico do segundo prisma
α = Ângulo entre os dois prismas
b = Ângulo entre o prisma A e o resultante prisma ( R )
R = Resultante ou o equivalente prisma.
Veja o Exemplo:





